Abstract
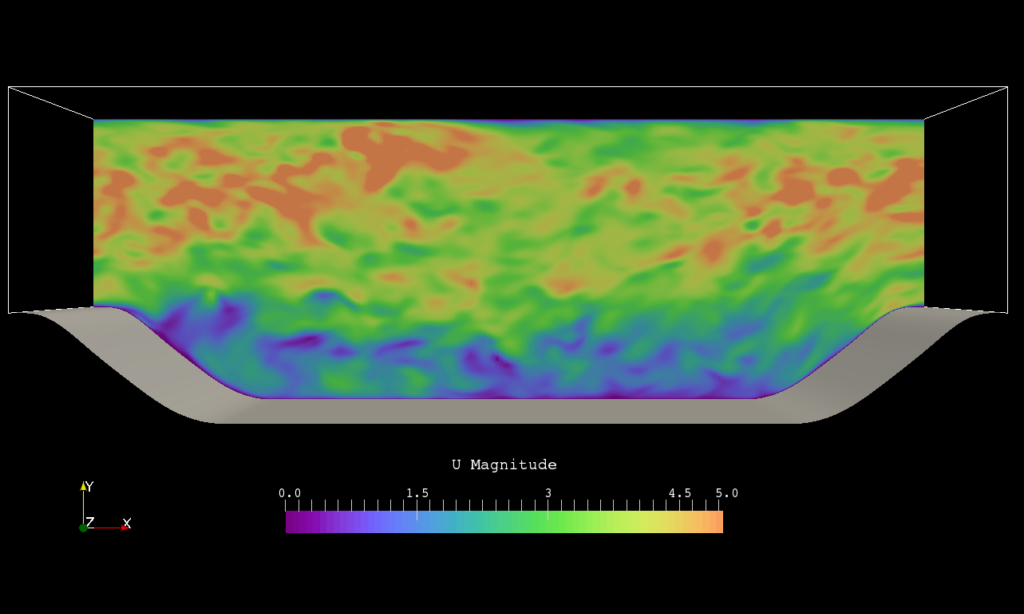
This paper presents a fast transient solver suitable for the simulation of transient turbulent flows. The main characteristic of the solver is that it is based on the projection method and requires only one pressure and the momentum solve per time step. Furthermore, using the projection method has the additional advantage that the formulation of the pressure equation is particularly efficient because the Laplacian term depends only on geometric quantities. This improves the parallel scalability of the Algebraic Multi-Grid (AMG) method because the coarse agglomeration levels can be cached if the grid is not changing and are consistent throughout each time step. The fractional step error near the boundaries is removed by utilizing the incremental version of the algorithm. The solver is implemented using v5.04 of the openly available Caelus computational mechanics library. Previous work by Stephens et al. demonstrated the accuracy of SLIM on several validation cases. In this work, performance of the solver was investigated through several test cases. The results indicate that SLIM has superior serial and parallel performance over the PISO and transient SIMPLE solvers. Transient solutions of incompressible, turbulent flows occupy an increasing portion of engineering computations. The majority of solvers that use the finite volume method on unstructured meshes with arbitrary number of faces per cell use either a transient SIMPLE or the PISO algorithm. While these algorithms are known to produce satisfactory spatial and temporal accuracy, they are not particularly efficient due to algorithmic constraints. Typically they require multiple solutions of the pressure equation (PISO algorithm) or multiple solutions of both momentum and pressure per time step (SIMPLE algorithm). In these algorithms, multiple solutions of the pressure and/or momentum equation per time step are required to remove the fractional step error due to splitting of equations and recover the time accuracy. Unlike the PISO and SIMPLE algorithms, the projection algorithm introduced originally by Chorin, does not require multiple pressure and momentum solves per time step. In this paper we describe an efficient implementation of the projection algorithm that can efficiently utilize the Algebraic Multi-Grid method for the pressure equation.