Abstract
Turbulence is a phenomenon that occurs frequently in nature and is present in almost all industrial applications. Despite significant increase in computational power in modern processors, Reynolds averaged Navier-Stokes (RANS) simulations are still the dominant approach to turbulence modelling of high Reynolds number flows. Hybrid LES/RANS approaches are currently used to offset the cost of Large Eddy Simulation (LES) computations by retaining the RANS characteristics in boundary layers while using the LES model away from walls. The hybrid approach embodied in the Detached Eddy Simulation (DES) methodology has been used with success in industrial flow simulations. However, it should be noted that the DES approach still requires LES-like mesh resolution away from walls. This is a simple consequence of the fact that the DES model defaults to LES at large distances from the walls. This may prove prohibitively expensive in simulations where large turbulent structures persists over most of the computational domain.
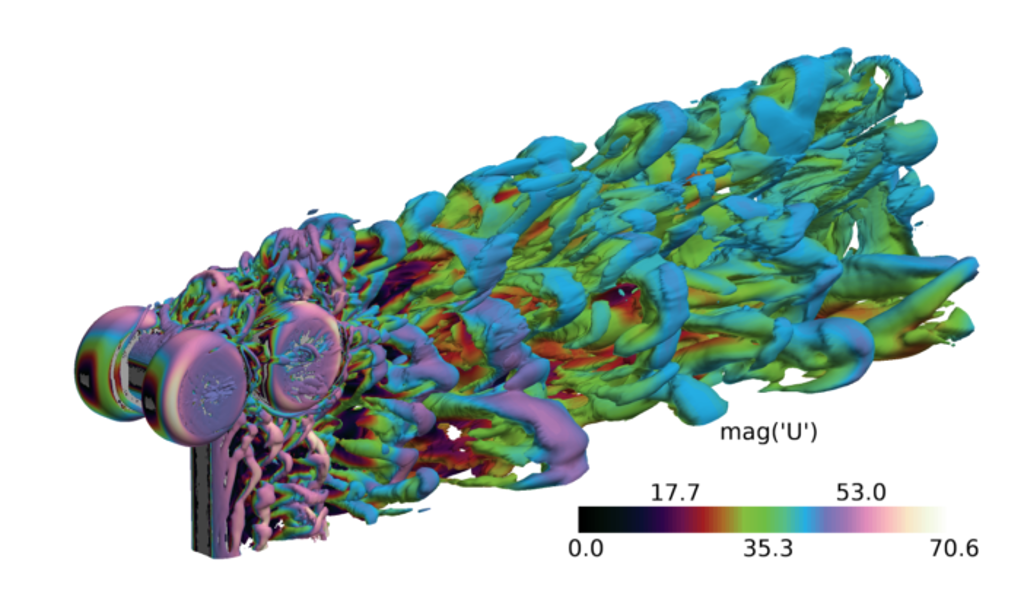
In this work, a delayed two equation very large eddy simulation (VLES) model based on three length scales is introduced. The resolution control function used to re-scale the Reynolds stresses is based on the ratio of the resolved to unresolved turbulence spectrum. The model constants are selected so that the Smagorinsky subgrid-scale model is recovered in the limit of grids approaching the resolution required for LES computations. The near wall RANS behaviour of the proposed model is obtained using blending functions. The objective was to implement this model using the open source library Caelus and validate the results against two test cases involving turbulent vortex shedding from a bluff-body. The test cases used were flow past a square cylinder at a Reynolds number of 21,400 and the Rudimentary Landing Gear benchmark case for Airframe Noise Computations (BANC).
The numerical simulations were carried out using a transient solver based on the open source computational mechanics library Caelus. The pressure-based solver with second-order bounded spatial discretisation and second-order bounded implicit time marching scheme was applied to obtain a time-accurate solutions. Compressibility effects were negligible for the Mach numbers under consideration and the flow was treated as incompressible. Results from the simulations indicate close agreement between the proposed model and available experimental and numerical results.